DIEZ PRUEBAS PARCIALES DE LA TEORÍA DE CUERDAS (I)
- planck
- 2 feb 2016
- 7 Min. de lectura
Actualizado: 27 dic 2024
Como es bien sabido la llamada teoría de cuerdas es nuestra mejor candidata para encontrar el "santo grial" de la Física fundamental: conseguir una teoría cuántica de la gravedad. Por si esto fuera poco las aspiraciones de la teoría van aún más allá: la teoría de cuerdas es la única teoría capaz de unificar las 4 fuerzas fundamentales de la naturaleza. También es sabido que, a fecha de hoy, no existe ninguna prueba experimental que permita validar o refutar esta "teoría". En este artículo veremos que esto no es del todo cierto. Es verdad que aún no existen pruebas experimentales sólidas a su favor pero sí que existen numerosos indicios, pruebas parciales, pruebas indirectas y "pruebas" matemáticas que nos indican claramente que la teoría de cuerdas tiene muchas probabilidades de explicar y unificar las cuatro fuerzas fundamentales del Universo. Hay que destacar que la "teoría" de cuerdas no es aún una teoría en el sentido más ortodoxo del método científico, realmente es un modelo teórico en construcción del cual aún no conocemos sus principios físicos fundamentales. Este hecho sin duda es una de las causas de que aún no se hayan podido encontrar predicciones claras que puedan ser comprobadas experimentalmente.
A continuación se describen diez de estas (semi)pruebas a favor de la validez de la teoría de cuerdas, el lector podrá juzgar por sí mismo hasta que punto estos indicios o pruebas parciales son indicadores de su validez.
1º) EL "CUANTO" DE LA GRAVEDAD APARECE DE FORMA NATURAL EN LA TEORÍA
El llamado modelo estándar (SM) es uno de los mayores logros de la Física fundamental y contiene todo lo que sabemos sobre Física de partículas. Uno de los pilares del SM es la teoría cuántica de campos (QFT) que sostiene que las entidades fundamentales son los campos y las partículas son vibraciones de estos campos. Resumiendo mucho en QFT se sigue la siguiente metodología:
1º) Se considera el lagrangiano de una partícula puntual. El lagrangiano no es más que la diferencia entre la energía cinética y la energía potencial.
2º) Se considera el trayecto seguido por la partícula entre dos puntos en el espacio-tiempo. Este trayecto será una linea.
3º) Se calcula la acción que no es más que la integral del lagrangiano entre los puntos inicial y final.
4º) Se calculan las ecuaciones del movimiento a partir de la fórmula de Euler-Lagrange. 5º) Se cuantizan las ecuaciones de movimiento para obtener sus "vibraciones", es decir, las partículas. En QFT las "vibraciones" se obtienen mediante una serie de operadores que actuan sobre el estado de mínima energía (el estado de vacío).
El SM contiene 3 de las 4 fuerzas fundamentales pero deja fuera la gravedad. Si intentamos incluir la gravedad incluyendo la métrica del espacio-tiempo siguiendo los principios de la relatividad general y la partícula cuántica de la gravedad (el gravitón) obtenemos que la mayoría de los resultados divergen, tienden a infinito. Esto es una
consecuencia directa de trabajar con entidades puntuales de dimensión 0 y radio 0. Por tanto es natural preguntarse:¿Que sucedería si en vez de considerar entidades puntuales (lo cual no puede ser más que una entelequia matemática y una aproximación a la realidad) consideramos entidades con cierta extensión, es decir,
diminutas "cuerdas" de dimensión 1? Veamos que es lo que sucede:
La ecuación de una onda que viaja en la dirección "y" de un plano a velocidad v es:

Consideremos ahora una cuerda de tensión To que es estirada una distancia muy pequeña:
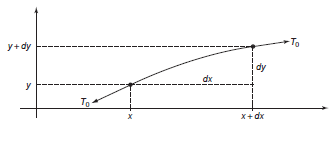
La fuerza neta aplicada horizontalmente es nula puesto que hemos cogido la cuerda de ambos extremos y le hemos aplicado la misma fuerza a ambos lados pero en dirección contraria. La fuerza neta es la aplicada en dirección vertical que será To veces la variación de y respecto de x en el punto x+dx menos la variación de y respecto de x en el punto inicial x, es decir:

Si igualamos esta expresión a la dada por la 2ª ley de Newton F=ma (µo es la densidad M/l) tenemos:

Eliminando dx en ambos lados y reordenando tenemos:

¡Esto no es más que la ecuación de una onda! Si la comparamos con la primera ecuación vemos que (µo/To)=(1/vo2). La solución a esta ecuación es la conocida función exponencial. Por la serie de Fourier podemos descomponer la función exponencial en sus armónicos o "vibraciones". Como veremos, estas vibraciones ¡se corresponden con las partículas conocidas!.
Siguiendo el método de trabajo de la QFT primero debemos obtener el lagrangiano de una cuerda que se mueve a la velocidad de la luz en el espacio-tiempo. Al considerar una cuerda que se mueve a la velocidad de la luz tenemos un "problemilla": no
existe conexión causal entre los "puntos" que constituyen la cuerda ya que al moverse a la velocidad de la luz no pueden "comunicarse" entre ellos. La solución es esclarecedora: no existen constituyentes fundamentales o "puntos" interiores en la cuerda, la cuerda es una entidad fundamental:
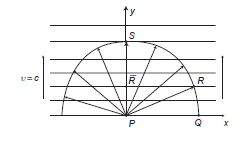
La cuerda que se mueve a la velocidad c en la dirección del eje Y. Si tomamos un punto P entonces el único punto alcanzable por P es aquel que se encuentra justo en la dirección de movimiento de la cuerda. El resto de puntos del semicírculo, incluidos el resto de "puntos" de la cuerda no son alcanzables por lo que están "desconectados" causalmente. Es imposible predecir como se mueven los "puntos" interiores a la cuerda de forma individual pero siempre podemos definir "un punto" en la cuerda que puede alcanzar otro punto cualquiera de la misma a la velocidad c. Esto nos permite describir el movimiento de la cuerda y nos indica que la cuerda es una entidad fundamental sin partes ni constituyentes interiores.
Una entidad de dimensión 1 o cuerda puede existir en 2 configuraciones: cuerda abierta o cuerda cerrada. Una cuerda abierta al viajar en el espacio-tiempo forma una superficie bidimensional en forma de hoja. Una cuerda cerrada forma un cilindro. La superficie de esta "hoja" es proporcional a la energía total de la cuerda.
La acción viene dada por la llamada acción de Nambu-Goto:

La ecuación de movimiento es simplemente:

La acción es simplemente la dinámica de 2 osciladores armónico simples. Las vibraciones de estos osciladores que son las vibraciones de la cuerda relativista forman un espectro continuo, sin embargo, cuando cuantizamos las ecuaciones sucede un "milagro": obtenemos un espectro discreto. ¡ Este espectro discreto se corresponde
con las partículas que conocemos!
Otro de los problemas que surgen es que para cada "modo de vibración" existen infinitas oscilaciones. Esto se resuelve mediante una técnica matemática llamada renormalización. Aquí interviene uno de los cálculos más famosos y más extraños de las Matemáticas "puras" aplicadas a la Física fundamental: el cálculo de la suma de
los infinitos números naturales. Para calcular un parámetro relacionado con la masa de la cuerda debemos calcular el valor de "a" tal que:

Donde D es el número de dimensiones del espacio-tiempo. Si aplicamos el famoso valor de -1/12 que se deriva de la aplicación de técnicas matemáticas como la función Z:

Entonces encontramos que a=-1/24(D-2). La invarianza Lorentz exige que a=-1 y por tanto que D=26. Es decir, la teoría de cuerdas solo es consistente en 26 dimensiones del espacio-tiempo, si consideramos supercuerdas en lugar de cuerdas el número de dimensiones del espacio-tiempo es 10. Esto es un problema, sin embargo, el hecho de que este número sea ÚNICO y el hecho que de que en realidad estas dimensiones
no sean macroscópicas sino grados de libertad microscópicos de las partículas hace esta posibilidad plausible. Consideremos ahora una cuerda cerrada. Para una cuerda cerrada el espectro es:

De forma similar a como las vibraciones de una cuerda de guitarra se pueden descomponer para distintos valores de la longitud de la cuerda (longitud de onda) el cuadro anterior representa los valores de los operadores del momento para diferentes valores del parámetro N que representa las diferentes oscilaciones o "vibraciones".
N=0 (0,0) corresponde al estado de vacío, es decir, sin vibraciones y sin partículas. Como veremos en el caso de las cuerdas abiertas, este estado presenta inestabilidades en forma de taquiones ya que se corresponde con estados de masa imaginaria. En el próximo apartado veremos como se soluciona este problema.
Para N=1 (1,1) obtenemos una partícula de masa 0 y de (D-2)2 estados de polarización. Esta partícula surge de aplicar una matriz de operadores a1i x a1j al estado de vacío |p+,pt|:

Esta matriz Rij es simétrica y sin traza. Para una matriz simétrica y sin traza el número de componentes es: n(D)=1/2(D-2)(D-1)-1=1/2D(D-3). En nuestro espacio-tiempo D=4 por tanto n(D)=2. Es decir, tenemos 2 grados de libertad. La matriz de polarización es una matriz de 2x2 y aunque parezca increíble ¡Esta matriz es igual a la que representa en relatividad general al tensor del campo gravitacional! Por tanto esta vibración corresponde a una partícula de masa 0 que tiene 2 grados de libertad con 2 polarizaciones diferentes. ¡Esta partícula es el gravitón! ¡ La primera vibración de una cuerda cerrada se corresponde con el "cuanto" de la gravedad !
Además, está matriz esconde otros 2 secretos. Sus componentes se pueden agrupar en 3 conjuntos linealmente independientes: los estados del gravitón y otros 2 conjuntos que representan 2 nuevos campos ocultos. Estos 2 campos son el llamado campo de Kalb-Ramond que representa la carga eléctrica y el campo Dilatón que determinará la amplitud de la interacción entre cuerdas.
2º) LA TEORÍA LOGRA UNIFICAR LAS 4 FUERZAS DE LA NATURALEZA
El hecho de que las 4 fuerzas fundamentales puedan ser incluidas en el marco teórico de la teoría de cuerdas constituye un hecho sorprendente y es otro indicio claro que apoya su validez. Para una cuerda abierta el espectro es:

La primera "vibración" N=0 representa a unas hipotéticas "partículas" de ¡Masa imaginaria! Estas "partículas" se denominan taquiones y se cree que no existen en la naturaleza. Esto fue un grave problema en las primeras versiones de la teoría de cuerdas, la solución apareció clara años más tarde: estas "partículas" representan la
desintegración de unas nuevas entidades: las branas. Los extremos de cuerdas abiertas están siempre unidos a branas.
La segunda "vibración" N=1 representa una partícula de masa 0 y con D-2 "estados de polarización". En nuestro espacio-tiempo D=4 por tanto la partícula tiene 2 estados de polarización. Esta partícula surge de aplicar el operador a1 sobre el estado de vacío |p+,pt|. Es decir:

El primer término representa los 2 estados de polarización. Tenemos entonces una partícula de masa 0 con dos estados de polarización: ¡ Esta partícula es el fotón !
El resto de partículas del modelo estándar se puede obtener con modelos de interacción entre branas y cuerdas.
Existen varios modelos que pueden generar las partículas que conocemos como por ejemplo éste.
En la próxima entrega veremos más (semi)pruebas de este marco teórico que promete toda una nueva revolución en la Física fundamental, entre ellas, la predicción de ¡Valores que pueden ser contrastados experimentalmente!
Fuentes: A first course in String Theory, Barton Zwiebach


Comments