Actualmente la teoría de supercuerdas (TSC) es nuestra mejor candidata a resolver el mayor problema de la física fundamental: fusionar en una sola teoría la mecánica cuántica y la relatividad general. Muchos críticos de la teoría de cuerdas afirman que esta teoría está demasiado desconectada del mundo físico real, es decir, de nuestro Universo actual de baja energía y que por tanto, es muy difícil que esta teoría pueda hacer predicciones comprobables experimentalmente. Aunque esto es cierto en la mayoría de casos (la TSC es una teoría de muy altas energías) existen ciertos casos muy concretos en los que esta teoría permite calcular el valor de magnitudes físicas de objetos que existen en nuestro Universo actual. En este artículo veremos, sin recurrir a matemáticas complejas, uno de esos casos, uno que permite establecer un espectacular vínculo entre la teoría de cuerdas y nuestro mundo real y que nos permite empezar a vislumbrar la respuesta al que probablemente es el enigma más grande de la Física: la naturaleza fundamental del espacio-tiempo.
Agujeros negros cargados eléctricamente
Dentro de la relatividad general podemos encontrar soluciones de agujeros negros (AN) esféricos sin carga ni rotación (AN de Schwarzschild), AN con carga eléctrica sin rotación (AN de Reissner-Nordstorm ) y AN con carga eléctrica y con rotación (AN de Kerr-Newman). En este artículo veremos el segundo caso. Estos agujeros negros tienen la siguiente métrica:

Esta métrica tiene dos horizontes: uno exterior r+ y otro interior r-. Este AN se describe únicamente con dos cargas: la masa M y la carga eléctrica Q. Existen tres casos posibles:
- M>Q: Este caso es físicamente el más común ya que los agujeros negros reales tienden a disminuir su carga eléctrica al consumir materia del exterior.
- M=Q: Este caso constituye lo que se denomina un agujero negro extremo. En este caso los dos horizontes r+ y r-coinciden y la radiación de Hawking es nula.
- M<Q: Este caso está descartado físicamente ya que da lugar a una singularidad desnuda (sin horizonte de sucesos) lo cual está prohibido por ciertas leyes de la física.
En este artículo nos centraremos en el segundo caso, ya que, como veremos, tiene unas propiedades especiales.
El problema de los microestados de un agujero negro
Los agujeros negros son, con mucha diferencia los objetos más extraños y fascinantes de nuestro Universo conocido. Desde el punto de vista clásico son objetos muy simples, se pueden describir solamente con tres magnitudes físicas: la masa, la carga eléctrica y el momento angular. Sin embargo, desde el punto de vista cuántico (semiclásico), los físicos han encontrado que estos objetos tienen una enorme entropía y que por tanto tienen una estructura interna y deben de estar compuestos por una enorme cantidad de elementos fundamentales: los microestados. Hawking y Bekenstein encontraron que esta entropía es S=A/4G donde A es el área del AN medido en unidades de planck. Esta paradoja representa de forma clara el problema de reconciliar la relatividad general con la mecánica cuántica. ¿Cual es el origen de estos microestados? ¿De que están compuestos? ¿Son estos microestados los objetos fundamentales que constituyen el espacio-tiempo? Aunque parezca increíble, existe un caso concreto, de un agujero negro real (1) en el que podemos contar estos microestados y "vislumbrar" su naturaleza. Esto es lo que haremos a continuación.
Los estados en la teoría de cuerdas
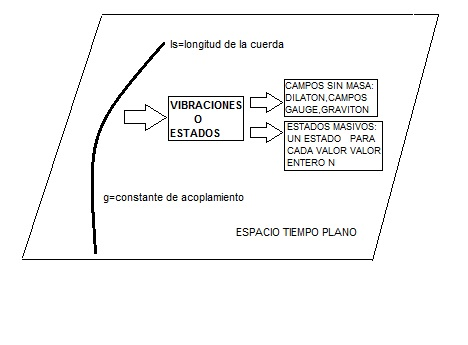
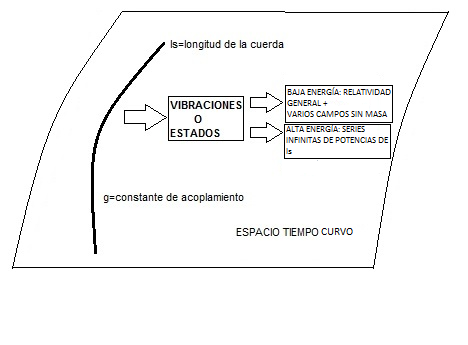
En la teoría de cuerdas encontramos que todas las partículas son vibraciones (estados) de un objeto unidimensional extendido (una cuerda). Si cuantizamos una cuerda en un espacio-tiempo plano obtenemos un conjunto finito de estados sin masa y un conjunto infinito de estados con masa (uno para cada valor entero N) con M2=N/ls2 (donde ls es la longitud de la cuerda). Si cuantizamos una cuerda en un espacio-tiempo curvo (típicamente una esfera o un toro) obtenemos un espacio-tiempo con la métrica de Einstein acoplado a una serie de campos sin masa más una serie infinita de términos de alto orden con potencias de ls. Cuando la curvatura es pequeña comparada con 1/ls2 entonces esta infinita serie de términos puede despreciarse. Si consideramos curvaturas pequeñas y ajustamos ciertos parámetros de forma que los campos escalares extra sean cero podemos resolver las ecuaciones de baja energía y obtener un espacio-tiempo equivalente al de la relatividad general. De hecho, obtenemos la siguiente métrica:

¡Esta es la métrica de un agujero negro extremo! (2) ¡Los AN extremos de las ecuaciones de Einstein son soluciones a las ecuaciones de la TSC!
De este resultado podemos deducir que un AN extremo es un estado de vibración muy masivo de una cuerda fundamental. Esto sucede porque cuando el acoplamiento supera un cierto valor el campo gravitatorio generado es tan grande que la cuerda colapsa formando un agujero negro. Todo esto puede verse resumidamente en las siguientes figuras:
Para el caso concreto de un AN extremo existen ciertos estados denominados estados BPS que permanecen invariantes tanto para acoplamientos débiles como para acoplamientos fuertes, como veremos, estos estados serán claves para estudiar los microestados de estos AN.
Además de la solución anterior existe otro tipo de soluciones a las ecuaciones de baja energía de la TSC: estas soluciones se conocen como solitones. Los solitones son soluciones estáticas y clásicas a las ecuaciones. En las teorías de campos los solitones
más conocidos son los monopolos y los propios agujeros negros. Como la TSC "vive" en un espacio-tiempo de 10 dimensiones los solitones pueden ser monopolos u objetos extendidos con horizonte (tipo AN) de varias dimensiones como las llamadas branas negras o "black p-branas".
Tipos de cargas en teoría de cuerdas
Como mencionamos anteriormente si aumentamos el acoplamiento de una cuerda (o de un gran número de cuerdas) por encima de cierto valor obtendremos un AN. Si este AN es extremo entonces, debido a la invarianza de los estados BPS con respecto al aumento del acoplamiento el sistema de cuerdas inicial y el agujero negro final ¡tendrán el mismo número de estados!

Nuestra primera tarea será identificar algún componente u "objeto" de la teoría de cuerdas que pudiera ser considerado como fundamental y que pueda ser contabilizado de alguna forma. Los principales candidatos que podrían cumplir este requisito son las cargas de la TSC. En la TSC existen dos tipos de cargas: las cargas NS-NS (por Neveu-Schwarz) y las R-R cargas (por Ramond). A alto acoplamiento obtenemos agujeros negros que pueden tener cargas NS-NS o cargas R-R pero con un acoplamiento fuerte no sabemos hacer cálculos precisos, si pudiéramos identificar que "objetos" son equivalentes a estas cargas a bajo acoplamiento quizás podríamos avanzar en la dirección correcta. ¿Que tipo de objetos son los equivalentes a las cargas NS-NS y R-R a bajo acoplamiento?
De forma similar a como un monopolo magnético porta una unidad de carga fundamental si el objeto que queremos identificar fuese un solitón portaría una unidad de carga. El objeto que porta una unidad de carga NS-NS a bajo acoplamiento es una vibración de una cuerda fundamental. Esto es coherente con la identificación anterior entre un AN y un estado masivo de un cuerda. Pero ¿cual es el equivalente a bajo g de una carga R-R? Inicialmente ningún objeto conocido parecía tener una unidad de carga R-R sin embargo, posteriormente los físicos encontraron el componente fundamental que estaban buscando: este era un "extraño" objeto extendido multidimensional cuyas vibraciones eran equivalentes a las de cuerdas abiertas con los extremos adheridos a ellos, estos objetos se denominaron D-branas. Estos objetos portan una unidad de R- carga y por tanto, en nuestra descripción, ¡podemos considerar a estos objetos como los objetos fundamentales que buscamos! ¡Empezamos a vislumbrar que estos "extraños" objetos extendidos podrían ser candidatos a constituir los microestados de los agujeros negros extremales. La pregunta clave ahora es: ¿Podemos contabilizar los estados de estos objetos fundamentales? ¿Si es así, coincidirá su valor con el predicho por la entropía de Bekenstein-Hawking?

Construyendo un agujero negro extremo con D-branas
A continuación queremos construir un AN extremo con D-branas para tratar de contabilizar el número de estados correspondientes a dicho AN. Por simplicidad construiremos un AN de 5 dimensiones en lugar de 4, sin embargo, también es posible construir de forma análoga un AN extremal en 4 dimensiones.
Si juntamos varias D-branas en un punto del espacio-tiempo estas formarán un estado ligado (de forma similar a como los electrones y el protón forman el estado ligado que constituye un átomo). Si tomamos este estado ligado de N D-branas con carga QN a bajo acoplamiento y aumentamos g entonces obtendremos un AN. Sin embargo, hay un problema: este AN tiene un horizonte singular, es decir, la métrica diverge y se hace infinita en el horizonte.

Para solucionar esto tenemos que considerar varios tipos de cargas en lugar de solo una. Consideremos ahora un estado inicial con D-branas que tienen dos tipos de cargas que denominaremos Q1 y Q5 (esta terminología quedará clara más adelante) que se juntan para formar un solo estado ligado BPS. Si ahora aumentamos g encontraremos que ¡ el horizonte del AN es finito! (3) ¡Ahora si tenemos un AN extremal real!
La pregunta que nos hacemos a continuación es: ¿Podemos interpretar físicamente estos estados ligados con carga Q1-Q5?
Para encontrar la respuesta consideraremos el espacio-tiempo natural de la TSC: un espacio-tiempo plano de 10 dimensiones. A continuación compactamos 4 dimensiones en un toro y 1 dimensión más en un círculo, de esta forma tenemos 5 dimensiones macroscópicas más un toro cuatro dimensional compactado en un círculo (total 5 dimensiones microscópicas). En las 5 dimensiones compactadas ¿que elementos fundamentales podríamos identificar con las cargas Q1 y Q5? Una D-brana enrollada en una dimensión compacta porta una unidad de R-carga (Q1) mientras que una D-brana enrrollada en 5 dimensiones compactas portaría otra unidad de R-carga (Q5). ¡Estos son los componentes fundamentales que forman nuestro agujero negro! Nuestro AN de 5 dimensiones está compuesto de un estado ligado de 1-branas y 5-branas.
La idea clave es la siguiente: existen muchos estados diferentes con la misma carga Q1Q5, si podemos contabilizar estos estados cuando g es pequeño podemos asegurar (debido a que los estados BPS se mantienen cuando g aumenta) que el AN tendrá el mismo número de estados. Al contabilizar cuantos estados tienen la misma carga Q1Q5 obtenemos que su número aumenta al aumentar el número de D-branas, en el límite en el que el número de branas es muy alto (tiende a infinito) encontramos que el número de estados crece exactamente como A/4G. ¡Esta es la entropía de Bekenstein-Hawking! ¡Esta es la conexión entre la teoría de cuerdas y los agujeros negros reales!
Conclusiones
Para darse cuenta de la importancia de este resultado hay que recordar que hemos partido de un estado ligado de muchos elementos que portan una unidad de carga fundamental en un espacio-tiempo plano (por tanto ni siquiera partimos de un horizonte para encontrar que S=A/4G) y hemos contabilizado la cantidad de estados diferentes con esta carga, independientemente de como compactemos las dimensiones extra o de de los detalles de como se forme el AN al aumentar g el número de estados inicial debe coincidir con el número de estados del AN final y este valor ¡coincide exactamente con la entropía de Bekenstein-Hawking! Esto es sin duda un impresionante éxito de la teoría de supercuerdas.
La teoría de cuerdas, como candidata a teoría cuántica de la gravedad nos permite ir más allá de cualquier estudio semiclásico y estudiar nuevos fenómenos físicos. Por ejemplo, la propia radiación de Hawking puede describirse, en ciertos modelos de cuerdas como el decaimiento de un estado no-BPS producido por la colisión de dos cuerdas abiertas que se mueven en sentido contrario dentro de una D-brana. Esta colisión produce una cuerda cerrada que abandona la brana situada en el horizonte lo que constituye la radiación de Hawking:

Otro ejemplo sería el hecho de que en ciertas descripciones basadas en D-branas las soluciones a las ecuaciones ¡continúan dentro del horizonte! de hecho, la situación en la que una cuerda cae dentro de un AN es descrita mediante el proceso en el que una cuerda (cerrada) se transforma en una cuerda abierta adjunta a una D-brana en el horizonte:

Por último, existen indicios de que cierto tipo de D-branas permiten cambiar la propia geometría-topología del espacio-tiempo donde residen dando lugar a nuevas configuraciones espacio-temporales (ver este artículo).
La apasionante aventura de encontrar los componentes más fundamentales que forman el Universo que habitamos continua y en esta búsqueda el marco Físico-Matemático de la teoría de cuerdas es, sin lugar a dudas, el que tiene más probabilidades de lograr la respuesta.
NOTAS
(1) En el Universo real un agujero negro cargado tendería a consumir matería de la carga opuesta y por tanto tendería a disminuir su carga. A pesar de esto, su existencia es teóricamente posible en ciertas condiciones muy concretas.
(2) Esta métrica es en realidad la de un agujero negro extremo en 5 dimensiones. Como se explica posteriormente en el artículo se ha escogido esta métrica unicamente por simplicidad y es perfectamente posible obtener la métrica de un agujero negro extremal de 4 dimensiones a partir de las ecuaciones de baja energía de la teoría de cuerdas.
(3) En realidad necesitamos 3 cargas para construir un agujero negro extremal con horizonte finito (la otra carga la formaría una cuerda con cierto momento en una dirección compacta) , sin embargo, a efectos prácticos, podemos considerar que las cargas fundamentales son las cargas Q1 y Q5.









Comments