Hace ya un tiempo que los Físicos y Matemáticos han descubierto que nuestro Universo es mucho más extraño y fascinante de lo que nadie hubiera imaginado. Aunque parezca imposible las Matemáticas y la Física moderna nos permiten, bajo ciertas circunstancias, tratar al infinito como si fuera una región más de nuestro Universo y realizar cálculos sobre magnitudes físicas que se pueden comprobar experimentalmente. ¡Podemos alcanzar y cuantificar el infinito!
Para poner las cosas aún más interesantes, recientemente los Físicos y Matemáticos han encontrado una fascinante estructura físico-matemática en el infinito, esta estructura posee nuevas simetrías y nuevas geometrías y lo que es más importante: podemos utilizarla para realizar cálculos sobre magnitudes físicas comprobables experimentalmente. En este artículo explicaremos las características de esta fascinante estructura que reside en el "borde infinito" de nuestro Universo.
Esferas celestes y cambios de coordenadas
Comenzaremos viendo el concepto de esfera celeste para un observador en un tiempo determinado. Definimos la esfera celeste como el conjunto de todos los objetos que son potencialmente observables (la luz ha tenido tiempo de llegar hasta el) por un observador en reposo en un momento determinado. Esto puede entenderse
intuitivamente como el cielo que vería un observador desde la Tierra con un telescopio infinitamente potente capaz de captar cada fotón de cualquier parte del Universo. Esto gráficamente se representa de la siguiente manera:

El observador situado en el punto C podrá ver la esfera de luz de radio r, ya que la luz tarda un tiempo en llegar hasta el. Si consideramos la esfera para r tendiendo a infinito obtendremos todo el cielo visible desde cualquier ángulo al que miremos. Este es el concepto Físico de esfera celeste.
El eje vertical representa el tiempo de la expansión del cono de luz. Los ejes horizontales se han girado 45º para hacerlos coincidir con el cono de luz mediante el cambio de coordenadas u=ct+r. El cono parte del punto A y se expande en todas direcciones a la velocidad de la luz. En el tiempo ct=B el cono de luz tendrá un radio r pero un observador en el punto B no podrá verlo en su totalidad ya que la luz no ha tenido tiempo de llegar a su posición, dicho observador tendrá que esperar hasta el tiempo ct=C para poder ver toda la esfera de luz de radio r (esto se representa mediante la flecha roja del dibujo). Por esto a este sistema de coordenadas se le llama coordenadas retardadas o coordenadas de Bondi. Si consideramos el cono de luz
para r tendiendo a infinito entonces obtenemos el concepto Físico de esfera celeste que contiene todos los puntos potencialmente visibles desde un punto en un instante de tiempo dado.

La esfera de Riemann
Considerar una esfera en el centro de coordenadas del plano complejo. A continuación trazamos una linea recta que una cada punto del plano con el polo Norte de la esfera. No es difícil ver que para cada punto del plano existe una y solo una recta que une ese punto con el polo Norte. Cada recta corta a la esfera en un punto diferente por lo que se concluye que ¡La esfera y el plano tienen exactamente los mismos puntos!

Todos los puntos de la (semi)esfera pueden ser proyectados en el plano complejo. Los puntos (los círculos) más cercanos al origen corresponden a los puntos más bajos de la esfera mientras que los puntos más lejanos del plano corresponden a puntos más altos. El polo norte es el punto situado en el infinito en el plano complejo.
Existe una única excepción: el polo Norte, este punto reside ¡en el infinito! A continuación veremos que relación hay entre el sistema de coordenadas del plano y el de la esfera.

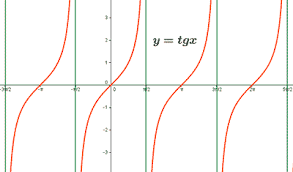
Las coordenadas P' en el plano y las de la esfera P están relacionadas por el siguiente cambio de coordenadas: X'= RX/(R-X3) y Y'= RY/(R-X3). Estas coordenadas se pueden agrupar en una sola coordenada compleja: Z'=(X+iY)/(R-X3) que en coordenadas polares se escribiría como: Z'= eiøtan(µ/2) donde ø es el ángulo polar y µ es el ángulo azimutal de la esfera. La función tan(µ) es una función asimptótica: a medida que nos alejamos
del centro nos aproximamos a +-PI/2 pero solo lo alcanzamos ¡ en el infinito!
Como el sistema de coordenadas de la esfera y del plano son equivalentes podemos usar uno u otro según nos convenga. Esto implica algo bastante sorprendente: en el sistema de coordenadas estereográficas, (la proyección en el plano) según avanzamos hacia el exterior, nos acercamos cada vez más a una especie de "borde" (el polo norte de la esfera) pero no lo llegamos a alcanzar: nos podemos acercar asimptóticamente a ese "punto" pero solo lo alcanzamos en el INFINITO.
Considerar el cono de luz expandiéndose de la primera figura de este artículo. Si cortamos al cono en rodajas horizontales cada una de ellas representa una esfera de radio r. Esto se puede representar en coordenadas estereográficas como un círculo en el plano complejo que va aumentado de radio y que se acerca a un valor situado en el "borde" de forma asimptótica sin llegar a alcanzarlo:
En esta representación los círculos interiores representan esferas situadas más atrás en el tiempo mientras que los círculos exteriores avanzan en el tiempo hacia el borde. El borde representa el infinito asimptótico (el polo norte de la esfera). ¡Este sería el "borde infinito" de nuestro Universo! Al cono de luz que representa el cono de luz pasado (la esfera celeste que ve un observador en un tiempo dado) se le denomina "Past Null Infinity" (I-). Al cono de luz que viaja hacia el futuro y que vería un hipotético
observador en el "borde infinito" se le denomina "Future Null Infinity" (I+). Esto se puede ver de forma esquemática en los llamados diagramas de Penrose:

El Future Null Infinity (I+) y el Past Null Infinity (I-) están situados a 45º (siguiendo los conos de luz) en el futuro y en el pasado. El Future Time Infinity (i+) y el Past Time Infinity (i-) están infinitamente separados en el tiempo futuro y pasado (t=infinito) y el Spacial Infinity (io) está infinitamente separado en el espacio (r=infinito)
Simetrías y cargas conservadas
Sabemos por el teorema de Noether que toda simetría global implica una cantidad física que se conserva. La simetría espacial implica la conservación del momento lineal, la simetría temporal implica la conservación de la energía, etc.
Fijémonos en nuestra esfera de Riemman anterior que es equivalente al plano complejo. ¿Cuales son las simetrías de la esfera? Es decir, ¿Que transformaciones dejan la esfera invariante? Las simetrías obvias de la esfera son las traslaciones y las rotaciones. Estas simetrías forman un grupo de simetría denominado grupo de Poincaré que juega un papel fundamental en las teorías relativistas. El grupo de Poincare incluye el grupo de Lorentz que es el grupo de simetría que relaciona dos sistemas de referencia inerciales en relatividad especial. Se puede demostrar Matemáticamente que el grupo de Lorentz es equivalente (isomorfo) al grupo de simetrías de la esfera que a su vez (como acabamos de ver) se puede proyectar en el plano complejo. Como dato curioso resulta que para dos observadores inerciales que se muevan a distintas velocidades (por ejemplo uno en reposo y otro a 0,9c) y que se mueven en la misma dirección, la relación entre ambos observadores en las coordenadas proyectadas en el plano es: Z´=e-xZ. Esto quiere decir que mientras que ambos están viendo la misma
esfera celeste, el observador Z´que se mueve a 0,9c verá la esfera celeste comprimida en torno a la dirección de movimiento. ¡El observador en movimiento verá las estrellas en la esfera celeste más juntas que el observador en reposo!
Una nave viajando a velocidades cercanas a las de la luz verá las estrellas del firmamento agrupadas alrededor de su dirección de movimiento.

La imagen que aparece en muchas películas de ciencia ficción cuando la nave protagonista alcanza velocidades cercanas a la de la luz no es correcta: la Física nos dice que los tripulantes deberían ver una contracción de la esfera celeste alrededor de la dirección
de movimiento (las estrellas se verían como puntos agrupados entorno al centro de la imagen).
Pero además de estas simetrías existe otra menos obvia: la simetría conforme. Básicamente es la simetría que deja invariante la esfera bajo cambios de escala (más concretamente las transformaciones que dejan los ángulos invariantes). Matemáticamente se puede demostrar que cualquier transformación de la forma Z(z)=az+b/cz+d forma parte de la simetría conforme. Es ahora cuando aparece lo más interesante: los Físicos han descubierto recientemente un nuevo grupo de simetrías que reside en la región "asimptótica" de nuestro Universo (lo que antes denominamos el "borde infinito) y como veremos pueden tener un papel fundamental en la resolución de muchos de los más grandes enigmas pendientes de la Física.
Viajando al "borde infinito" del Universo
Como vimos anteriormente, las coordenadas polares (coordenadas de la esfera) y las coordenadas estereográficas (coordenadas de la proyección de la esfera en el plano) están relacionadas por la función tg(x) que es una función asimptótica.
Sin embargo, este cambio de coordenadas no es único, existen otros cambios que implican diferentes funciones asimptóticas. Por ejemplo, el campo electromagnético o el campo gravitatorio decaen como 1/r2 con la distancia r. Esto implica un comportamiento asimptótico ya que el campo solo será nulo cuando r tiende a infinito. Pues bien, al conjunto de todos los posibles espacio-tiempos que decaen asimptóticamente a 0 en el infinito se les denomina espacio-tiempos asimptóticamente planos. El conjunto de todos estos espacio-tiempos (el conjunto de sus propiedades cuánticas) forman un grupo de simetría (ya que estos dejan invariantes ciertas propiedades) llamado grupo BMS. Este grupo opera en el "null infinity" y es mucho más grande que el grupo de Poincare, de hecho, es un grupo infinito y por tanto da lugar a una infinita cantidad de cargas conservadas. Las transformaciones que permiten pasar de un elemento a otro del grupo BMS se denominan supertraslaciones.
Las infinitas cargas se traducirían en un número infinito de nuevas partículas que se denominan "soft gravitons" en el caso del campo gravitatorio y "soft photons" para el caso del campo electromagnético. Estas partículas vivirían en el "Null Infinity" y poseerían energía y momento nulos, sin embargo, (esto aún se está investigando) podrían tener una polarización-momento angular y por tanto podrían portar información. Estas "soft particles" podrían tener la respuesta a uno de los interrogantes más profundos de la Física fundamental: la paradoja de la información de los agujeros negros: estas partículas también se encontrarían en el horizonte de los agujeros negros (que también es una superficie nula como I+) y podrían constituir el soporte físico donde queda almacenada la información de la materia que cae en el agujero negro. La famosa frase acuñada por el Físico John Wheeler de "los agujeros negros no tienen pelo" podría ser falsa": quizás estos tienen una cantidad infinita de "pelo". La existencia de estas hipotéticas partículas y sus características es actualmente uno de los campos de investigación más activos e importantes de la Física teórica.

Conjunto de cargas intercambiando "Soft Photons"
Podría parecer que todo esto es solo una estructura Matemática sin consecuencias para la Física sin embargo esto no es cierto: codificada en la geometría asimptótica del Null Infinity está almacenada la información sobre el momento y la energía de las ondas gravitatorias que han sido radiadas desde el pasado hasta el Future Null Infinity (I+). Calculando estos datos almacenados en el Null Infinity obtenemos las ecuaciones que describen las ondas gravitatorias de la teoría de la relatividad general en su formulación exacta no lineal. Estas son las ecuaciones que se han utilizado para modelar las recientemente descubiertas ondas gravitacionales y por tanto describen magnitudes Físicas reales comprobables experimentalmente.
Por último hay que señalar que la dualidad AdS/CFT relaciona un espacio tiempo con gravedad en 4 dimensiones con una teoría cuántica de campos conforme en 3 dimensiones. Esta última reside ¡en el borde infinito del Universo AdS! y contiene
toda la información necesaria para describir el Universo 4D. Nuestro Universo no es AdS sino (aproximadamente) dS ,sin embargo, hay una intensa investigación en marcha para descubrir las características de una dualidad dS/CFT. ¿Podría ser que, siguiendo este principio holográfico, toda la información de nuestro Universo 4D resida en el borde infinito? ¡ La Física y las Matemáticas modernas nos permiten alcanzar y cuantificar el "borde infinito" de nuestro Universo donde quizás resida la respuesta a gran parte de los grandes misterios de la naturaleza a nivel fundamental!




Comentários